un grafo G, es un par ordenado de V y A, vértices y aristas.
un vértice puede tener 0 o mas aristas
una arista debe unir a dos vertices
aristas
son las lineas que se unen y con la que construye caminos.- Aristas Adyacentes: Dos aristas son adyacentes si convergen en el mismo vértice.
- Aristas Paralelas: Son paralelas cuando el vértice inicial y el final son el mismo.
- Aristas Cíclicas: Es cuando una arista parte de un vértice para entrar en el mismo.
- Cruce: Son dos aristas que cruzan en un punto.
vertices
son los puntos o nodos con los que esta conformado un grafo.
- Vértices Adyacentes: si tenemos un par de vértices de un grafo (U, V) y si tenemos un arista que los une, entonces U y V son vértices adyacentes y se dice que U es el vértice inicial y V el vértice adyacente.
- Vértice Aislado: Es un vértice de grado cero.
- Vértice Terminal: Es un vértice de grado 1.
caminos
El número de aristas del camino se llama la longitud del camino.
Si los vértices no se repiten el camino se dice propio o simple.
Cuando los dos extremos de un camino son iguales, el camino se llama circuito o camino cerrado.
Llamaremos ciclo a un circuito simple
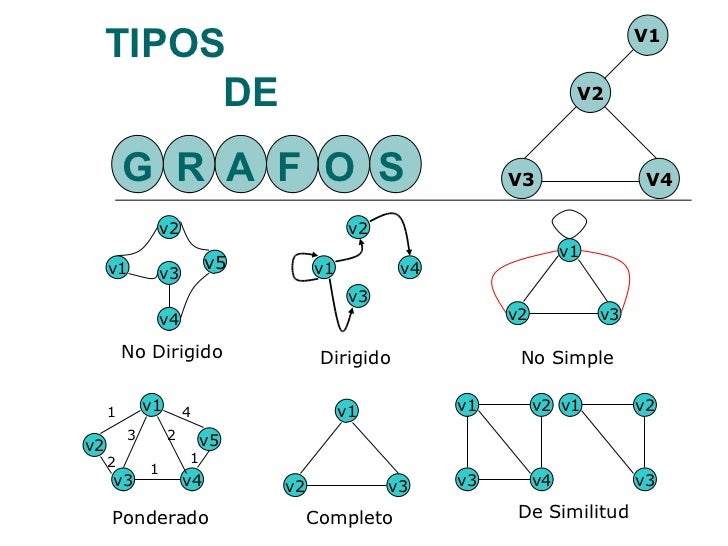

clasificación de grafos
se pueden clasificar en dos grupos: dirigidos y no dirigidos
- Grafo regular: Aquel con el mismo grado en todos los vértices
- Grafo bipartito: Es aquel con cuyos vértices pueden formarse dos conjuntos disjuntos de modo que no haya adyacencias entre vértices pertenecientes al mismo conjunto.
- Grafo completo: Aquel con una arista entre cada par de vértices.
- Grafo nulo: Se dice que un grafo es nulo cuando los vértices que lo componen no están conectados, esto es, que son vértices aislados.
- Grafos Isomorfos: Dos grafos son isomorfos cuando existe una correspondencia biunívoca (uno a uno), entre sus vértices de tal forma que dos de estos quedan unidos por una arista en común.
- Grafos Platónicos: Son los Grafos formados por los vértices y aristas de los cinco sólidos regulares (Sólidos Platónicos), a saber, el tetraedro, el cubo, el octaedro, el dodecaedro y el icosaedro.
grafos conexos
un grafo se puede definir como conexo si cualquier vertice pertenece al conjunto de vertices y es alcanzable por algun otro
recorrido de un grafo
recorrer un grafo es tratar de alcanzar todos los nodos que esten relacionados con uno que llamaremos nodo de salida.
grafo dirigido
se le define a un grafo que contiene aristas dirigidas
los siete puentes de konigsberg
fue lo que dio origen a la teoría de grafos.
En la ciudad de Königsberg hay una isla y el río Pregel que la rodea se divide en dos brazos. La distintas zonas de tierra están unidos mediante siete puentes (color rojo). ¿Es posible dar un paseo por la ciudad, empezando por cualquiera de las cuatro partes de tierra firme, cruzando cada puente una y sólo una vez y volver nuevamente al punto de partida?.
Después de un tiempo, en 1736, Leonhard Euler dio respuesta a este problema, dando origen a la teoría de grafos.
Euler se dio cuenta que la cantidad de líneas de cada punto tendría que ser par, para así poder entrar y salir de dicho punto, ocupando tan solo una vez cada puente.
En el problema de Königsberg, Euler demostró que era imposible recorrer la ciudad de la forma pedida, ya que el número de líneas que llegan a cada punto es impar y ésto implica que no es posible recorrerlos pasando una sola vez por cada uno de los puentes, es decir, no había solución para ese problema.

En la ciudad de Königsberg hay una isla y el río Pregel que la rodea se divide en dos brazos. La distintas zonas de tierra están unidos mediante siete puentes (color rojo). ¿Es posible dar un paseo por la ciudad, empezando por cualquiera de las cuatro partes de tierra firme, cruzando cada puente una y sólo una vez y volver nuevamente al punto de partida?.
Después de un tiempo, en 1736, Leonhard Euler dio respuesta a este problema, dando origen a la teoría de grafos.

Euler se dio cuenta que la cantidad de líneas de cada punto tendría que ser par, para así poder entrar y salir de dicho punto, ocupando tan solo una vez cada puente.
En el problema de Königsberg, Euler demostró que era imposible recorrer la ciudad de la forma pedida, ya que el número de líneas que llegan a cada punto es impar y ésto implica que no es posible recorrerlos pasando una sola vez por cada uno de los puentes, es decir, no había solución para ese problema.
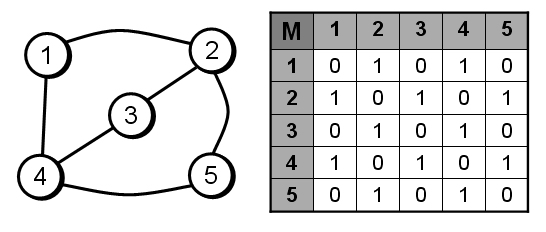
formas de representación
matriz adyacente: se asocia cada fila y cada columna a cada nodo del grafo, siendo la relación entre los mismo tomando 1 si existe la arista y 0 si no existe
Lista de adyacencias: se asocia a cada nodo del grafo una lista que contenga todos aquellos nodos que sean adyacentes a él.